常用激活函数和损失函数
目录
sigmod
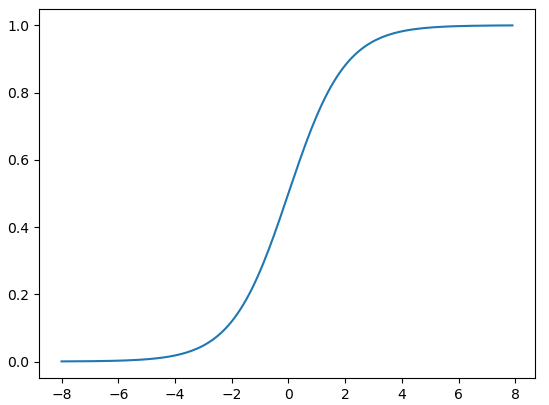
定义:
$$
\sigma(x) = \frac{1}{1+e^{-x}}
$$
求导:
$$
\sigma' = \sigma(x)(1-\sigma(x))
$$
softmax
作为分类问题输出层的激活函数
将各个输出节点的输出值范围映射到[0, 1],并且约束各个输出节点的输出值的和为1
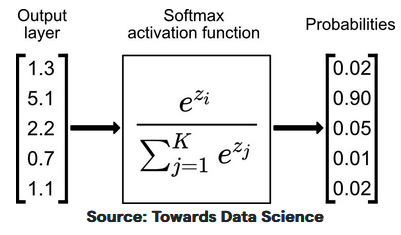
定义:
$$
softmax(z_i) = \frac{e^{z_i}}{\sum ^{K}_{j=1}e^{z_j}}
$$
求导:设$softmax(z_i) = p_i$
$$
\frac{\partial y_i}{\partial z_j} =
\begin{cases}
p_i(1-p_j) &j=i\\
-p_j\cdot p_i &j\neq i
\end{cases}
$$
交叉熵损失函数
softmax通常配合交叉熵损失函数使用
$$
p_i = softmax(z_i) = \frac{e^{z_i}}{\sum ^{K}_{j=1}e^{z_j}}
$$
定义:$y_i$是真实样本标签值,分类问题里不是0就是1
$$
L=- \sum ^K_{i=1}y_i\log(p_i)
$$
求导:
$$
\frac{\partial L}{\partial z_i} = p_i - y_i
$$
求导非常简单,所以softmax和交叉熵一起用,反向传播时候计算就非常简单了