TinyRenderer笔记4:着色器
顶点着色器和片段着色器
OpenGL 2的渲染管道可以表示如下(新版本也差不多):
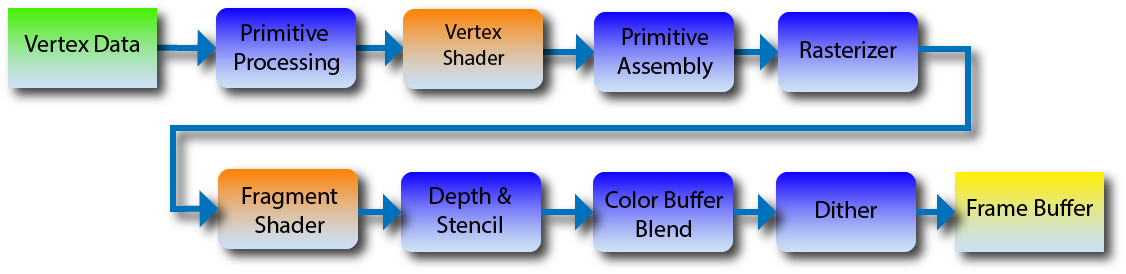
在较新的OpenGL中还有其他着色器,在这个课程中只关心顶点着色器(vertex shader)和片段着色器(fragment shader)。
在上面图片中,我们无法触摸的阶段都用蓝色表示,我们的回调用橙色表示。
事实上现在的main()函数是原始的处理程序(primitive processing routine),它可以叫做顶点着色器。我们在这里没有primitive assembly的步骤,由于我们仅绘制三角形在我们的代码中,它与primitive processing合并。现在的triangle()函数是是rasterizer,对于在三角形中的每个像素都调用了了片段着色器的功能,然后执行深度检查之类的。
知道了什么是着色器就可以开始创建着色器了。
顶点着色器的主要目标是变换顶点的坐标,第二个目标是为片段着色器准备数据。
片段着色器的主要目标是确定当前像素的颜色,次要目标是我们可以通过返回true丢弃当前像素。
着色器的定义:
pub trait IShader {
/// 顶点着色器
/// iface 第i个面, nth_vert 面的第n个顶点
/// 返回顶点在裁剪空间的坐标(齐次坐标)
fn vertex(&mut self, i_face: usize, nth_vert: usize) -> glm::Vec4;
/// 片段着色器
/// bar 当前像素在三角形中的重心坐标 color 像素颜色
/// 返回true表示丢弃当前像素
fn fragment(&mut self, bar: Vec3, color: &mut image::Rgba<u8>) -> bool;
}实现一个着色器
实现一个简单的Gouraud着色器:
pub struct GouraudShader<'a> {
model: &'a obj::Obj<TexturedVertex, u32>,
varying_intensity: glm::Vec3, // 强度变化,由顶点着色器写入,由片段着色器读取
view_port: Mat4,
projection: Mat4,
model_view: Mat4,
light_dir: Vec3,
}
impl<'a> GouraudShader<'a> {
pub fn new(
model: &'a obj::Obj<TexturedVertex, u32>,
model_view: Mat4,
projection: Mat4,
view_port: Mat4,
light_dir: Vec3,
)// 实现省略;
}
impl<'a> IShader for GouraudShader<'a> {
fn vertex(&mut self, i_face: usize, nth_vert: usize) -> glm::Vec4 {
let i_vert = self.model.indices[i_face * 3 + nth_vert];
let vert = self.model.vertices[i_vert as usize];
let normal = Vec3::from_array(&vert.normal);
let v = Vec3::from_array(&vert.position);
let gl_v = self.view_port * self.projection * self.model_view * v.extend(1.);
self.varying_intensity[nth_vert] = glm::dot(*normal, self.light_dir).max(0.); // 计算每个顶点的光照强度
gl_v
}
fn fragment(&mut self, bar: glm::Vec3, color: &mut image::Rgba<u8>) -> bool {
let intensity = glm::dot(self.varying_intensity, bar); // 当前像素的插值强度,重心坐标计算相对三个顶点的强度
let x = (255. * intensity) as u8;
*color = image::Rgba([x, x, x, 255]);
return false; // 不丢弃任何像素
}
}使用这个着色器,重新实现main函数绘制模型:
fn main() {
let eye = glm::vec3(0., -1., 3.); // camera
let center = glm::vec3(0., 0., 0.);
let up = glm::vec3(0., 1., 0.);
let light_dir = glm::normalize(glm::vec3(1., 1., 1.));
let (width, height) = (800, 800);
let mut image = ImageBuffer::<Rgba<u8>, _>::from_pixel(width, height, BLACK);
let mut zbuffer = ImageBuffer::<Luma<u8>, _>::from_pixel(width, height, Luma([0]));
let model = obj::load_obj::<obj::TexturedVertex, _, u32>(input).unwrap();
let model_view = lookat(eye, center, up);
#[rustfmt::skip]
let projection = glm::mat4(
1., 0., 0., 0.,
0., 1., 0., 0.,
0., 0., 1., -1./ glm::distance(eye, center),
0., 0., 0., 1.);
let view_port = viewport(
width as i32 / 8,
height as i32 / 8,
width as i32 * 3 / 4,
height as i32 * 3 / 4,
);
// 创建着色器
let mut shader = GouraudShader::new(&model, model_view, projection, view_port, light_dir);
// 遍历每个面
for i in 0..model.indices.len() / 3 {
let mut screen_coords: [glm::Vec4; 3] = [glm::Vec4::zero(); 3];
// 遍历每个面的每个顶点
for j in 0..3 {
screen_coords[j] = shader.vertex(i, j);
}
triangle_with_shader(
screen_coords[0],
screen_coords[1],
screen_coords[2],
&mut shader,
&mut image,
&mut zbuffer,
);
}
flip_vertical_in_place(&mut image);
image.save("a.png").unwrap();
flip_vertical_in_place(&mut zbuffer);
zbuffer.save("b.png").unwrap();
}在遍历每个顶点时,调用顶点着色器,在对三角行进行栅格化的时候会调用片段着色器:
/// 注意现在输入的顶点坐标是齐次坐标
pub fn triangle_with_shader<
I: GenericImage<Pixel = Rgba<u8>>,
I2: GenericImage<Pixel = Luma<u8>>,
S: IShader,
>(
a_4d: glm::Vec4,
b_4d: glm::Vec4,
c_4d: glm::Vec4,
shader: &mut S,
image: &mut I,
zbuffer: &mut I2,
) {
let a = v4p2v3(a_4d); // a b c是齐次坐标投影到屏幕上的坐标
let b = v4p2v3(b_4d);
let c = v4p2v3(c_4d);
// 确定枚举像素的边界
let bboxmin = glm::vec2(a.x.min(b.x).min(c.x).max(0.), a.y.min(b.y).min(c.y).max(0.));
let bboxmax = glm::vec2(
a.x.max(b.x).max(c.x).min(image.width() as f32 - 1.),
a.y.max(b.y).max(c.y).min(image.height() as f32 - 1.),
);
for px in bboxmin.x as i32..=bboxmax.x as i32 {
for py in bboxmin.y as i32..=bboxmax.y as i32 {
let bc_screen = barycentric(a, b, c, glm::vec3(px as f32, py as f32, 0.));
// 留意下这里,z和w都使用齐次坐标算的
let z = glm::dot(glm::vec3(a_4d.z, b_4d.z, c_4d.z), bc_screen);
let w = glm::dot(glm::vec3(a_4d.w, b_4d.w, c_4d.w), bc_screen);
let frag_depth = (z / w + 0.5) as u8;
let frag_depth = frag_depth.min(255).max(0);
if bc_screen.x < 0. || bc_screen.y < 0. || bc_screen.z < 0. {
continue;
}
let mut color = image::Rgba([0; 4]);
let discard = shader.fragment(bc_screen, &mut color);
let idx = px + py * image.width() as i32;
let zb: &mut Luma<u8> = zbuffer.get_pixel_mut(px as _, py as _);
if zb.0[0] <= frag_depth {
zb.0[0] = frag_depth;
if !discard {
image.put_pixel(px as u32, py as u32, color);
}
}
}
}
}最终画出来的图片如下,一个模型,一个zbuffer的灰度图:
| a.png | b.png |
|---|---|
 |
 |
这里是完整代码: 11e8d2cbfc251d694bb65ae40ec463b54636b0c0
修改片段着色器
令强度仅具有6个值:
let eye = glm::vec3(1., 1., 3.); // camera
let center = glm::vec3(0., 0., 0.);
let up = glm::vec3(0., 1., 0.);
let light_dir = glm::normalize(glm::vec3(1., 1., 0.9));
fn fragment(&mut self, bar: glm::Vec3, color: &mut image::Rgba<u8>) -> bool {
let mut intensity = glm::dot(self.varying_intensity, bar);
intensity = if intensity > 0.85 {
1.
} else if intensity > 0.6 {
0.8
} else if intensity > 0.45 {
0.6
} else if intensity > 0.3 {
0.45
} else if intensity > 0.15 {
0.3
} else {
0.
};
*color = image::Rgba([(255. * intensity) as u8, (155. * intensity) as u8, 0, 255]);
return false;
}查看变化

纹理
现在只计算了每个点的光照,修改着色器带上纹理:
varying_uv: glm::Mat3, // 三个顶点的纹理坐标
fn vertex(&mut self, i_face: usize, nth_vert: usize) -> glm::Vec4 {
let i_vert = self.model.indices[i_face * 3 + nth_vert];
let vert = self.model.vertices[i_vert as usize];
let normal = Vec3::from_array(&vert.normal); // 顶点法向量
let v = Vec3::from_array(&vert.position); // 顶点位置
let uv = Vec3::from_array(&vert.texture); // 纹理坐标
let gl_v = self.view_port * self.projection * self.model_view * v.extend(1.);
self.varying_intensity[nth_vert] = glm::dot(*normal, self.light_dir).max(0.); // 计算每个顶点的光照强度
self.varying_uv.as_array_mut()[nth_vert] = uv.clone(); // 每一列是一个顶点出的纹理坐标
gl_v
}
fn fragment(&mut self, bar: glm::Vec3, color: &mut image::Rgba<u8>) -> bool {
let intensity = glm::dot(self.varying_intensity, bar); // 当前像素的插值强度,重心坐标计算相对三个顶点的强度
let uv = self.varying_uv * bar; // 用重心坐标插值当前点的纹理坐标
let px = self.diffuse.get_pixel(
(uv.x * self.diffuse.width() as f32) as _,
(uv.y * self.diffuse.height() as f32) as _,
);
let r = (px[0] as f32 * intensity) as u8;
let g = (px[1] as f32 * intensity) as u8;
let b = (px[2] as f32 * intensity) as u8;
*color = image::Rgba([r, g, b, 255]);
return false; // 不丢弃任何像素
}查看结果:

代码:81b8c2ae2d04f70036f8ef4227f9bb2ffd5a519a
几种着色方法介绍
- 平面(Flat)着色: 每个三角形只计算一个光照
- Gouraud着色: 每个三角形计算三个顶点的光照,使用三个顶点的光照对三角形中每个点做线性插值
- Phong着色: 我们把三角形的每个点的法向量都插值出来,然后再计算光照
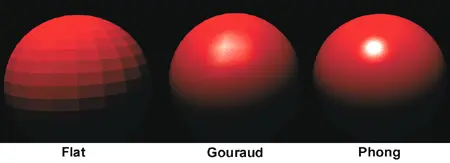
法线贴图(Normal Mapping)
我们有纹理坐标,和这样的纹理贴图。

除了纹理,也可以把几乎任何东西存进纹理图像中。它可以是颜色、方向、温度等等。
让我们加载这个纹理:

如果我们将RGB值解释为xyz方向,该图像为我们提供了每个渲染像素的法向量,这样我们就不用靠三个顶点的法向量来插值法向量了。
需要注意,如果对模型进行了仿射变换,那么法向量需要做映射才能使用,上篇有讲,结论:法向量的变换矩阵为模型变换矩阵的逆转置矩阵。
也有一些表示方式能直接描述切空间中的法向量。在达布坐标系中,z向量垂直于物体,x是主曲率方向,y是它们的叉积。
下面是使用纹理映射的例子:
从这里新建了一个Phong着色器的实现
diffuse_nm: &'a ImageBuffer<Rgba<u8>, Vec<u8>>, // 法线贴图
uniform_m: Mat4, // 模型的变换矩阵m projection*model_view
uniform_mit: Mat4, // m的逆转置矩阵 m.inverse().transpose()
fn vertex(&mut self, i_face: usize, nth_vert: usize) -> glm::Vec4 {
let i_vert = self.model.indices[i_face * 3 + nth_vert];
let vert = self.model.vertices[i_vert as usize];
let normal = Vec3::from_array(&vert.normal); // 顶点法向量
let v = Vec3::from_array(&vert.position); // 顶点位置
let uv = Vec3::from_array(&vert.texture); // 纹理坐标
let gl_v = self.uniform_m * v.extend(1.);
self.varying_uv.as_array_mut()[nth_vert] = uv.clone(); // 每一列是一个顶点出的纹理坐标
gl_v
}
fn fragment(&mut self, bar: glm::Vec3, color: &mut image::Rgba<u8>) -> bool {
let uv = self.varying_uv * bar; // 用重心坐标插值当前点的纹理坐标
let px = self.diffuse.get_pixel(
(uv.x * self.diffuse.width() as f32) as _,
(uv.y * self.diffuse.height() as f32) as _,
);
let nm_px = self.diffuse_nm.get_pixel(
(uv.x * self.diffuse.width() as f32) as _,
(uv.y * self.diffuse.height() as f32) as _,
);
let mut n = Vec3::from_array(&[nm_px[0] as _, nm_px[1] as _, nm_px[2] as _]).clone(); // 从贴图中加载法向量
n.as_array_mut()
.iter_mut()
.for_each(|v| *v = *v / 255. * 2. - 1.); // tga图像中[0,255], 转换到[-1,-1]
let n = self.uniform_mit * n.extend(0.); // 法线映射 注意向量转换位齐次坐标是填0
let n = glm::normalize(vec4_to_3(n)); // 齐次坐标投影回3d 注意向量不需要除w分量
let l = self.uniform_m * self.light_dir.extend(0.); // 之前是在顶点作色器中计算光照,现在要在切空间计算
let l = glm::normalize(vec4_to_3(l));
let intensity = glm::dot(n, l);
let r = (px[0] as f32 * intensity) as u8;
let g = (px[1] as f32 * intensity) as u8;
let b = (px[2] as f32 * intensity) as u8;
*color = image::Rgba([r, g, b, 255]);
return false; // 不丢弃任何像素
}需要注意的点是向量再参与齐次坐标运算时,w分量需要是0,计算后投影回3d时xyz不需要除以w分量。
这里再贴下点和向量映射回来时的区别:
/// 齐次坐标系中的点投影到3d
/// 点坐标需要除以w
pub fn v4p2v3(v: glm::Vec4) -> glm::Vec3 {
glm::vec3(v.x / v.w, v.y / v.w, v.z / v.w)
}
/// 齐次坐标系中的向量投影到3d
/// 向量坐标不需要除以w
pub fn vec4_to_3(v: glm::Vec4) -> glm::Vec3 {
glm::vec3(v.x, v.y, v.z)
}结果:
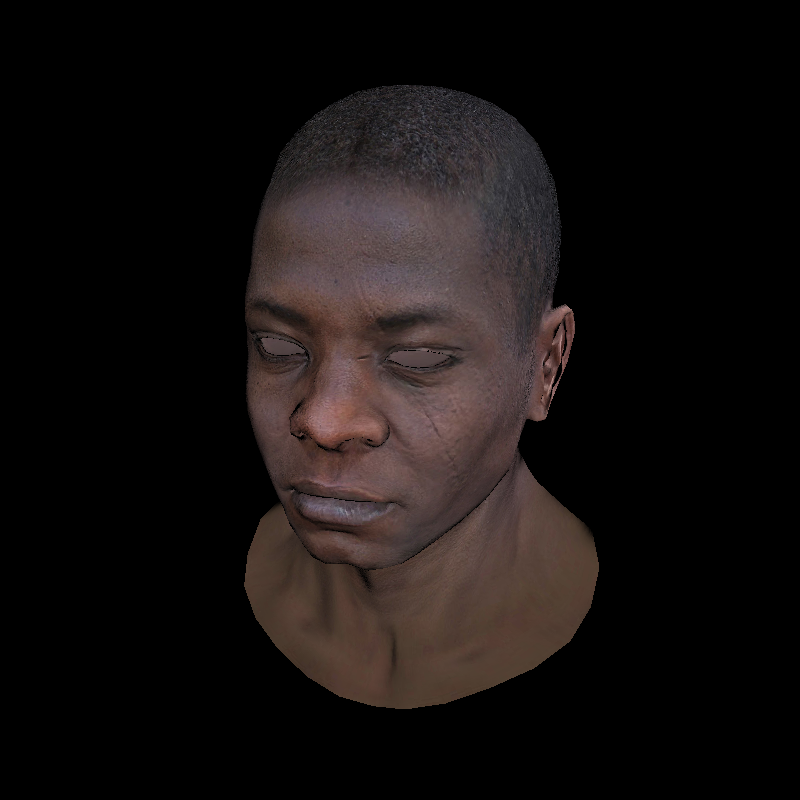
可以看到皮肤的起伏细节相较于只用三个顶点的法向量插值要好的多。
代码:951f42ea125a28c4f7e7aa83573d68fd43cef472
上面得到的图片比作者的亮,后来发现是全局光照进不进行矩阵变换的区别。再次修改代码
// let l = self.light_dir.extend(0.); // 之前是在顶点作色器中计算光照,现在要在切空间计算
// let l = glm::normalize(vec4_to_3(l));
let l = self.light_dir; // 全局光照不进行矩阵变换
let intensity = glm::dot(n, l);结果:

代码:64d58b1c6d0569db3db1eefaead38443d05b9ac9
高光贴图(Specular Mapping)
Phong光照模型:
Phong提议将最终照明视为三个光强度的加权总和:环境光(ambient lighting)、漫反射光(diffuse lighting)、镜面光(specular lighting)

我们前面计算的光都是漫反射光,计算了光方向向量和法线向量的余弦值。这假设了光在各个方向上均匀反射。如果是光滑的表面比如镜面,光反射范围会更小,只有反射到了我们的眼睛内我们才能看见。
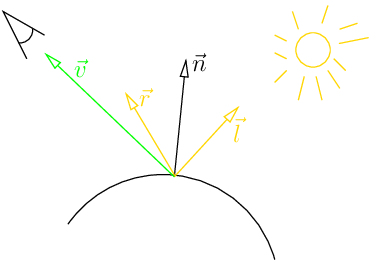
对于漫反射光我们关心的是向量$n$和向量$l$的余弦值,现在我们要开始关注反射光$r$和视角方向$v$之间的夹角。
给出$n$和$l$如何求$r$:glm::normalize(n * (glm::dot(n, l) * 2.) - l)
光滑的表面在一个方向上的反射比在其他方向上的反射要多,如果我们使用余弦值的$n$次方会怎样${\cos \theta }^{n}$,所有小于1的数在进行幂运算时都会减小,这意味这余弦的$n$次方会使反射光的半径变小。不同材质的反射表现,这个信息可以存在高光贴图中。他告诉我们每个点是否有光泽。
diffuse_spec: &'a ImageBuffer<Rgba<u8>, Vec<u8>>, // 高光贴图
fn fragment(&mut self, bar: glm::Vec3, color: &mut image::Rgba<u8>) -> bool {
let uv = self.varying_uv * bar; // 用重心坐标插值当前点的纹理坐标
let px = self.diffuse.get_pixel(
(uv.x * self.diffuse.width() as f32) as _,
(uv.y * self.diffuse.height() as f32) as _,
);
let nm_px = self.diffuse_nm.get_pixel(
(uv.x * self.diffuse_nm.width() as f32) as _,
(uv.y * self.diffuse_nm.height() as f32) as _,
);
let spec_px = self.diffuse_spec.get_pixel(
(uv.x * self.diffuse_spec.width() as f32) as _,
(uv.y * self.diffuse_spec.height() as f32) as _,
);
let spec_v = spec_px[0] as f32 / 1.; // 光泽值, 这个值越小越反射范围越大,越不光泽,越大越有光泽
let mut n = Vec3::from_array(&[nm_px[0] as _, nm_px[1] as _, nm_px[2] as _]).clone(); // 从贴图中加载法向量
n.as_array_mut()
.iter_mut()
.for_each(|v| *v = *v / 255. * 2. - 1.); // tga图像中[0,255], 转换到[-1,-1]
let n = self.uniform_mit * n.extend(0.); // 法线映射 注意向量转换位齐次坐标是填0
let n = glm::normalize(vec4_to_3(n)); // 齐次坐标投影回3d 注意向量不需要除w分量
let l = self.uniform_m * self.light_dir.extend(0.); // 映射光照方向
let l = glm::normalize(vec4_to_3(l));
let r = glm::normalize(n * (glm::dot(n, l) * 2.) - l); // 反射光方向
let spec = glm::pow(r.z.max(0.), spec_v); // 我们从z轴看, dot(v,r)
let diff = glm::dot(n, l).max(0.);
let arg_ambient = 5.; // 环境光
let arg_diffuse = 1.; // 漫反射光
let arg_specular = 0.6; // 镜面反射光
let intensity = glm::dot(n, l);
let r = (arg_ambient + px[0] as f32 * (arg_diffuse * diff + arg_specular * spec)) as u8;
let g = (arg_ambient + px[1] as f32 * (arg_diffuse * diff + arg_specular * spec)) as u8;
let b = (arg_ambient + px[2] as f32 * (arg_diffuse * diff + arg_specular * spec)) as u8;
*color = image::Rgba([r, g, b, 255]);
return false; // 不丢弃任何像素
}这些参数都是可以调整的,不同的选择会给对象带来不同的外观
let arg_ambient = 5.; // 环境光
let arg_diffuse = 1.; // 漫反射光
let arg_specular = 0.6; // 镜面反射光
结果如下: