在欧几里得空间中，一个坐标可以由一个原点和基底给出，考虑点$P$在坐标系$(O,i,j,k)$中拥有坐标$(x,y,z)$的含义，它意味着向量$\overrightarrow{OP}$ 可以表示为:
$$
\overrightarrow{OP}=\vec{i}x+\vec{j}y+\vec{k}z =
\begin{aligned}
\begin{bmatrix}
\vec{i}& \vec{j}& \vec{k}
\end{bmatrix}
\end{aligned}
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
$$
现在我们有另外一个坐标系$(O,i',j',k')$，如何将坐标从一个坐标系转换到另一个坐标系，首先$(i,j,k)$和$(i',j',k')$是三维的基底，存在一个(非简并)矩阵$M$使得：
$$
\begin{aligned}
\begin{bmatrix}
\vec{i'}& \vec{j'}& \vec{k'}
\end{bmatrix}
\end{aligned}
=
\begin{aligned}
\begin{bmatrix}
\vec{i}& \vec{j}& \vec{k}
\end{bmatrix}
\end{aligned}
\times M
$$
参考下面的例子
让我们重新表示$\overrightarrow{OP}$：
$$
\overrightarrow{OP} = \overrightarrow{OO'} + \overrightarrow{O'P}
=
\begin{aligned}
\begin{bmatrix}
\vec{i}& \vec{j}& \vec{k}
\end{bmatrix}
\end{aligned}
\begin{bmatrix}
O'_{x} \\ O'_{y} \\ O'_{z}
\end{bmatrix}
+
\begin{aligned}
\begin{bmatrix}
\vec{i'}& \vec{j'}& \vec{k'}
\end{bmatrix}
\end{aligned}
\begin{bmatrix}
x' \\ y' \\ z'
\end{bmatrix}
$$
现在把右边的$(i',j',k')$替换成矩阵
$$
\overrightarrow{OP}
=
\begin{aligned}
\begin{bmatrix}
\vec{i}& \vec{j}& \vec{k}
\end{bmatrix}
\end{aligned}
\left(
\begin{bmatrix}
O'_{x} \\ O'_{y} \\ O'_{z}
\end{bmatrix}
+
M
\begin{bmatrix}
x' \\ y' \\ z'
\end{bmatrix}
\right)
$$
它给出了坐标从一个坐标系到另一个坐标系的变换公式
$$
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
=
\begin{bmatrix}
O'_{x} \\ O'_{y} \\ O'_{z}
\end{bmatrix}
+
M
\begin{bmatrix}
x' \\ y' \\ z'
\end{bmatrix}
\
\Rightarrow
\
\begin{bmatrix}
x' \\ y' \\ z'
\end{bmatrix}
=
M^{-1}
\left(
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
-
\begin{bmatrix}
O'_{x} \\ O'_{y} \\ O'_{z}
\end{bmatrix}
\right)
$$
目前我们实现的渲染器相当于使用位于Z轴上的摄像机来绘制场景。如果我们想要移动摄像机得到不同视角的画面，没问题，我们可以移动所有的场景，而不移动摄像机。
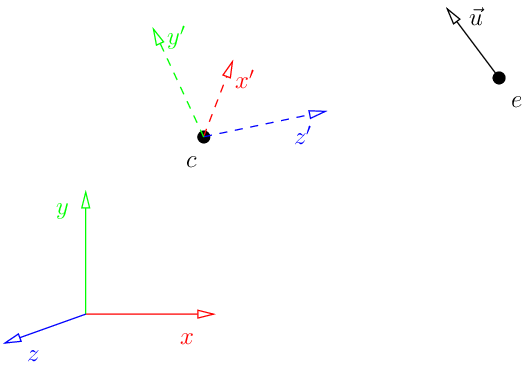
让我们这样来看待这个问题：我们想画一个场景，相机位于点$e$(眼睛)。相机应对准点$c$(中心)，向量$u$(up)指向画面的上方：
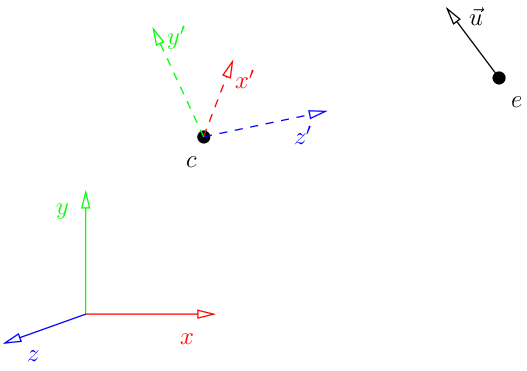
这意味着我们要在坐标系$(c,x',y',z')$中渲染，但是我们的模型是在$(O,x,y,z)$中给出的，这没有问题，我们只需要计算坐标的变换。这是rust代码计算必要的4x4矩阵ModelView：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
// eye 摄像机位置 center 焦点 up视角上方
fn lookat(eye: glm::Vec3, center: glm::Vec3, up: Vec3) -> glm::Matrix4<f32> {
let z = glm::normalize(eye - center); // 向量ce
let x = glm::normalize(glm::cross(up, z)); // 同时垂直于 up和z的向量
let y = glm::normalize(glm::cross(z, x));
// 注意glm中是按列存的
#[rustfmt::skip]
let minv = glm::mat4(
x.x, y.x, z.x, 0.,
x.y, y.y, z.y, 0.,
x.z, y.z, z.z, 0.,
0., 0., 0., 1.,
);
#[rustfmt::skip]
let tr = glm::mat4(
1., 0., 0., 0.,
0., 1., 0., 0.,
0., 0., 1., 0.,
-eye.x, -eye.y, -eye.z, 1.,
);
minv * tr
}
|
想象原点$O$平移到$c$ ,然后通过旋转$O$的坐标轴，使得坐标轴$xyz$于$x’y’z'$重合。“我们可以移动所有的场景，而不移动摄像机。"
正常理解是摄像机旋转，然后平移：(旋转、平移可以操作可以叠加成一个矩阵，写成乘法是从后往前写)
$$
M_{camera}=M_{translation}\ *\ M_{rotation}
$$
我们用它来看物体，可以摄像机不动，对物体做上面变换的逆变换：
$$
M^{-1}_{camera}=M^{-1}_{rotation}\ *\ M^{-1}_{translation}
$$
旋转矩阵的逆是它的转置，平移矩阵的逆也就是再吧它移回去。
rust代码中写的矩阵是这么来的：
$$
lookat =
\begin{aligned}
\begin{bmatrix}
R_{x}& R_{y}& R_{z}& 0\\
U_{x}& U_{y}& U_{z}& 0\\
D_{x}& D_{y}& D_{z}& 0\\
0& 0& 0& 1
\end{bmatrix}
\end{aligned}
\begin{aligned}
\begin{bmatrix}
1& 0& 0& -P_x\\
0& 1& 0& -P_y\\
0& 0& 1& -P_z\\
0& 0& 0& 1
\end{bmatrix}
\end{aligned}
$$
- R - 右向量，对应相机坐标系x轴在世界坐标中的表示
- U - 上向量，对应相机坐标系y轴在世界坐标中的表示
- D - 方向向量，对应相机坐标系z轴在世界坐标中的表示
- P - 相机在世界坐标系中的位置
我们在代码中写过这样的转换
1
2
3
4
5
|
let screen_coords_a = glm::vec3(
((a.x + 1.) * (width) as f32),
((a.y + 1.) * (height) as f32),
a.z,
);
|
我们有一个点$a$，它属于正方形$[-1,1]*[-1,1]$，我们想要把它画成$(width,height)$尺寸的图像。
$a.x + 1$的范围在0到2，$(a.x+1)/2$的范围在0到1，$(a.x+1)*width/2$刚好适配图像尺寸。
接下来要替换掉这种丑陋的方式，把所有的计算写成矩阵形式。
Viewport矩阵：
$$
\begin{aligned}
\begin{bmatrix}
\frac{w}{2}& 0& 0& x+\frac{w}{2}\\
0& \frac{h}{2}& 0& y+\frac{h}{2}\\
0& 0& \frac{d}{2}& \frac{d}{2}\\
0& 0& 0& 1
\end{bmatrix}
\end{aligned}
$$
它意味着立方体$[-1,1][-1,1][-1,1]$映射到屏幕立方体$[x,x+w][y,y+h][0,d]$其中d是深度对应z轴。作者说：是的，立方体，而不是矩形，这是因为Z-Buffer的深度计算。这是Z-Buffer的分辨率。我喜欢将其等于255，因为简单地将Z-Buffer的黑白图像进行调试。，暂时还不知道这句话含义。
上面的矩阵也很好推倒，他可以拆分为：
- 平移：把$[-1,1][-1,1][-1,1]$平移到$[0,2][0,2][0,2]$
- 缩放：$[0,2][0,2][0,2]$缩放到$[0,1][0,1][0,1]$
- 缩放：$[0,1][0,1][0,1]$缩放到$[0,w][0,h][0,d]$
- 平移：$[0,w][0,h][0,d]$平移到$[x,x+w][y,y+h][0,d]$
$$
\begin{aligned}
\begin{bmatrix}
1& 0& 0& x\\
0& 1& 0& y\\
0& 0& 1& 0\\
0& 0& 0& 1
\end{bmatrix}
\end{aligned}
\begin{aligned}
\begin{bmatrix}
w& 0& 0& 0\\
0& h& 0& 0\\
0& 0& d& 0\\
0& 0& 0& 1
\end{bmatrix}
\end{aligned}
\begin{aligned}
\begin{bmatrix}
\frac{1}{2}& 0& 0& 0\\
0& \frac{1}{2}& 0& 0\\
0& 0& \frac{1}{2}& 0\\
0& 0& 0& 1
\end{bmatrix}
\end{aligned}
\begin{aligned}
\begin{bmatrix}
1& 0& 0& 1\\
0& 1& 0& 1\\
0& 0& 1& 1\\
0& 0& 0& 1
\end{bmatrix}
\end{aligned}
$$
最终结果就是viewport矩阵
1
2
3
4
5
6
7
8
9
10
11
12
|
fn viewport(x: i32, y: i32, w: i32, h: i32) -> glm::Matrix4<f32> {
let (x, y, w, h) = (x as f32, y as f32, w as f32, h as f32);
let d = 255.;
#[rustfmt::skip]
let m = glm::mat4(
w/2., 0., 0., 0.,
0., h/2., 0., 0.,
0., 0., d/2., 0.,
x+w/2., y+h/2., d/2., 1.,
);
m
}
|
模型一般在他们的本地坐标系中被创建(object coordinates)，他们被插入世界坐标(world coordinates)表达的场景，从一个位置转换到另一个是用矩阵Model进行的。然后，我们想在相机坐标系(eye coordinates)中表达它，这个转换叫做View。然后使用投影矩阵(Projection)对场景进行透视变形，这个矩阵将场景转换为所谓的裁剪坐标(clip coordinates)。最后，我们绘制场景，将裁剪坐标转换为屏幕坐标的矩阵称为Viewport。
如果我们从.obj文件中读取点v，那么为了在屏幕上绘制它，它将经历以下转换链：
1
|
Viewport * Projection * View * Model * v.
|
当我们只画一个对象时，Model不做用任何事情(我们不需要更改对象在世界中的位置)，可以忽略。
1
2
3
4
|
let fin =view_port * projection * model_view;
let a = v4p2v3(fin * a.extend(1.));
let b = v4p2v3(fin * b.extend(1.));
let c = v4p2v3(fin * c.extend(1.));
|
暂时画出来长这样：
代码见这里44bf1901d7d4cea9e3c8a7b01a88e6fcddaa7206
如果我们有一个模型，并且其法向量由艺术家给出，如果我们使用该模型进行了仿射变换，那么不能简单的对其原有法向量进行相同的变换。
简单的例子就是如$p(1,0)$是模型的某个法向量，我们把模型沿y轴平移1个单位，如果也对法向量进行平移操作得到$p'(1,1)$，显然$p'$和$p$不是平行的.
具体可以看这里：知乎
结论：法向量的变换矩阵为模型变换矩阵的逆转置矩阵
$$
M'=(M^{-1})^T
$$